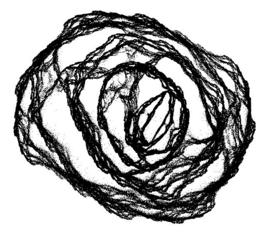
 Some snap shots of Second Julia set for regular polynomial maps
Some snap shots of Second Julia set for regular polynomial maps
 Some snap shots of Second Julia set for regular polynomial maps
Some snap shots of Second Julia set for regular polynomial maps
Skew product family
Pictures for skew product maps ( c = 0 in the following family):
X = x^2 + a*x + b*y
Y = y^2 + c*x + d*y
In this family, a=-2, c=0, d=-2 are fixed. Parameter b is varied from 0 to two thirds. For b=0, the base dynamics, Y=y^2-2*y, and the fiber dynamics, X=x^2-2*x, have interval from -1 to 3 as their Julia sets. So, the second Julia set of the product dynamics is a square in the real plane.
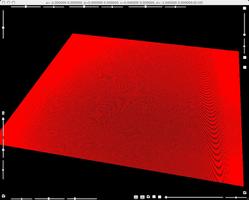
A square second Julia set for product map for parameters a=-2, b=0, c=0,d=-2.
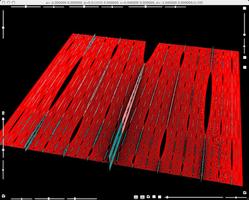
A square second Julia set is broken by varying parameter b slightly.
For non zero parameter b, The dynamical system is a skew product.
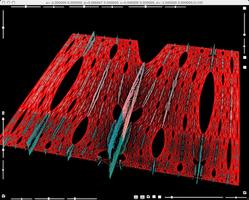
Parameter b is varied furhter.
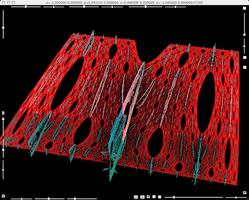
Parameters b varied still further.
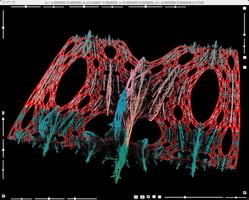
Parameters b varied still further.
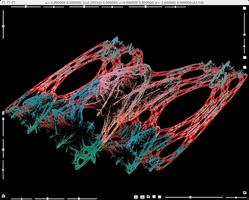
Parameters b varied still further.
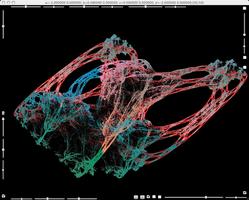
Parameters b varied still further.

Parameters b varied still further. Side view of the second Julia set.
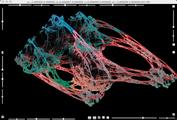
A snap shot of second Julia set for skew product map for parameters a=-2,b=0.4667,c=0,d=-2.
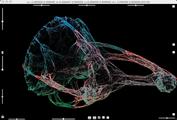
A snap shot of second Julia set for skew product map for parameters a=-2,b=0.6667,c=0,d=-2.
Some further deformation of the second Julia set.
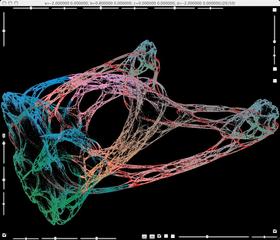
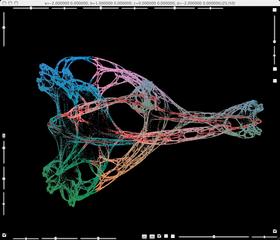
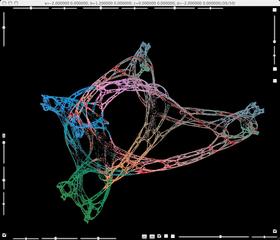

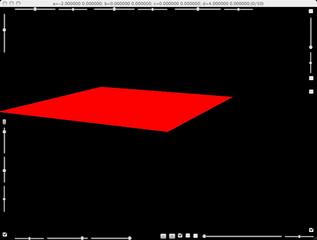
This family begins with a square of second Julia set.
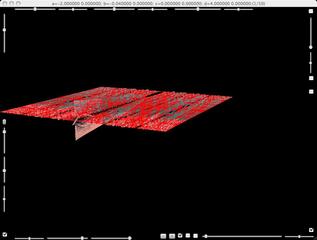
By a slight change of parameters, fences and branches emanate from the square.
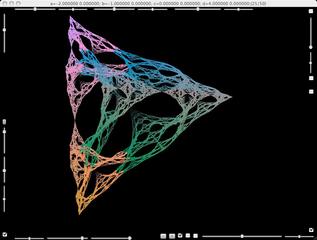
This second Julia set looks like the Sierpinskii Gasket.
Most of the points have four preimages.
This dynamics does not satisfy the so-called "open set condition".
In this family, our regular polynomial maps is postcomposed with a linear map.
The parameters for this linear maps are not indicted in the title line of the windows of StereoViewer.