b=-0.12, c=-1.124. Just before homoclinic tangency.
In these programs, periodic points are computed after Biham-Wenzel's method. The Runge-Kutta method for this computation was programed by Mr. Kuya. Deep points, i.e., points near the Julia set, are chosen as follows. Take many points in the unstable manifold of a saddle (fixed or periodic) point and pick up points which need many times of iterations before escaping out of a big ball. To find points in Siegel disks or Siegel-Reinhardt domains, try many randomly chosen initial points and find very long bounded orbits. Take the middle parts of the very long bounded orbits. Rigorously saying, these methods are not mathematically well justified. But it seems that these pictures are well consistent with our understandings of Julia sets. Some aspects are even beyond our imaginations.
Family of complex Henon maps for B=-0.12 (i.e. det(H) = 0.12), with c=-0.8 to -1.4. Homoclinic tangency is observed for c near -1.13.
b=-0.12, c=-1.124. Just before homoclinic tangency.
b=-0.12, c=-1.136. Just after homoclinic tangency.
Family of complex Henon maps for B=-1.0 (i.e. det(H) = 1), with c=2.0 to -6.0. This family is well known as the area preserving Henon map in the real plane. In the real plane, depending on the parameter values, there exist KAM circles surrounding the elliptic fixed point. Between KAM circles, as Poincre's famous picture indicates, there are periodic saddle points and homoclinic points. Observe that the unstable manifolds and stable manifolds of saddle periodic points intersect inbetween the KAM circle and many points in the Julia sets are found there. Horseshoe structure can also be observed in this family. In these pictures, skyblue points represent periodic points and other points of other colors represent orbits of randomly chosen initial points whose iterates stay bounded for very long time.
Red points are in the real plane. KAM circles are observed in this snap shot.
KAM circles and elliptic islands are obserced in the real plane.
For this parameter, the fixed point becomes parabolic. Behavior of the dynamics near the parabolic fixed point is interesting.
KAM circles and elliptic islands are obserced in the real plane.
KAM circles and elliptic islands are obserced in the real plane.
KAM circles and elliptic islands are obserced in the real plane.
KAM circles and elliptic islands are obserced in the real plane.
KAM circles and elliptic islands are obserced in the real plane.
Family of complex Henon maps for B=0.3 (i.e. det(H) = -0.3), with c=-0.8 to -1.6. Henon's strange attractor appears in the real plane for parameter c=-1.3 (a=1.4 in Henon's original family).
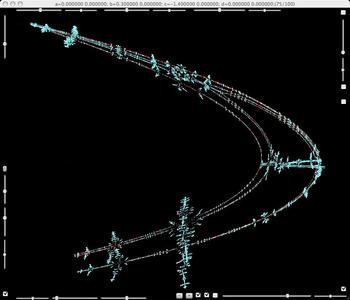b=0.3, c=-1.4. Parameter value for Henon's strange attractor.
Red points are in the real plane.
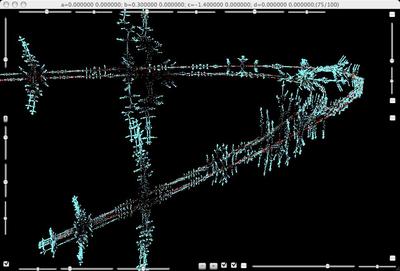b=0.3, c=-1.4. Enlargement of the pruned branches of the strange attractor.
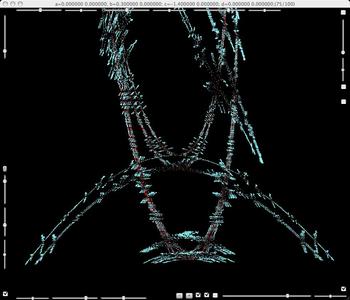b=0.3, c=-1.4. Same Julia set from different viewpoint.
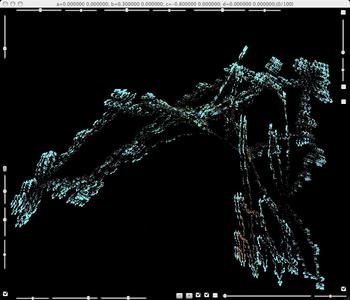b=0.3, c=-0.8. There is an attracting fixed point.
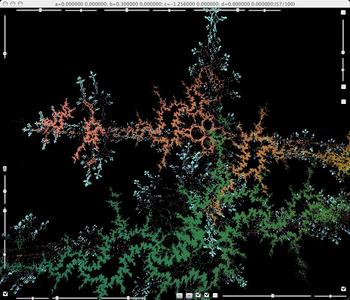b=0.3, c=-1.256. Coexistence of attractors.
Family of complex Henon maps for B=1.0 (i.e. det(H) = -1.0), with c=0 to -2.
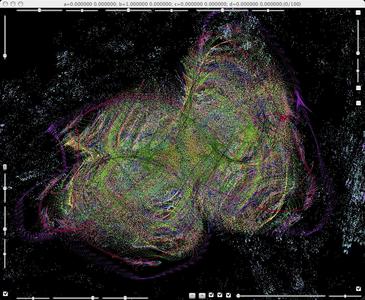b=1, c=0. The origin is a parabolic fixed point with eigenvalues 1 and -1.
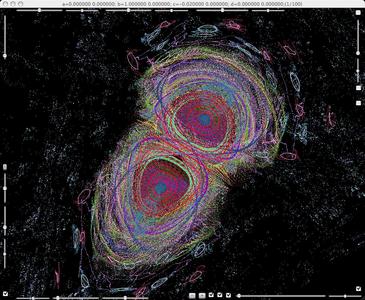b=1, c=-0.02. KAM circles and homoclinic points appear.
Family of complex Henon maps for B=0.3 (i.e. det(H) = -0.3), with c varied so that one of the eigen value of a fixed point has modulus one with diophantian rotation numbers. Siegel's theorem says that there exist a disk holomorphically embedded in the dynamical space passing by the fixed point and invariant under the action of the dynamical system.
Family of complex Henon maps for B=-0.3 (i.e. det(H) = 0.3), with c varied so that one of the eigen value of a fixed point has modulus one with diophantian rotation numbers. Siegel's theorem says that there exist a disk holomorphically embedded in the dynamical space passing by the fixed point and invariant under the action of the dynamical system.
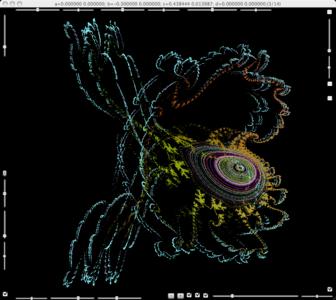b=-0.3, c= 0.438444+0.013987i.
Family of complex Henon maps for B=0.9 (i.e. det(H) = -0.9), with c varied so that one of the eigen value of a fixed point has modulus one with diophantian rotation numbers. Siegel's theorem says that there exist a disk holomorphically embedded in the dynamical space passing by the fixed point and invariant under the action of the dynamical system.
Family of complex Henon maps for abs(det(H))=1. Parameters are chosen so that both of the eigenvalues at a fixed point are of mudulus one and their rotation numbers are rationally independent. The eigenvalues hopefully satisfy the Siegel's linearizability condition. Around the fixed point, the dynamical system is holomorphically conjugate to a product of rigid rotations of ratinally independent rotation numbers. The orbit of each initial point sufficiently near the fixed point is embedded in a torus. Each torus bounds a polydisc. And the union of such orbits form a Reinhardt domain. I call this invariant domain a Siegel-Reinhardt domain. More precisely a Siegel-logarithmically-convex-complete-Reinhardt domain.
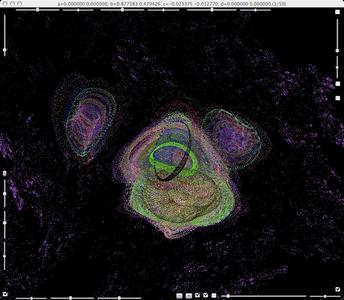b=0.877583+0.479426i, c=-0.023375-0.01277i. Observe tori.
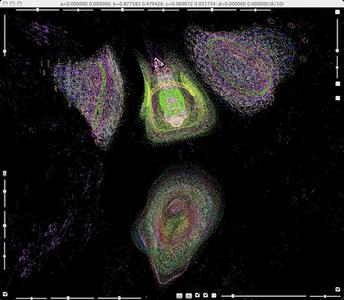b=0.877583+0.479426i, c=-0.069072+0.037734i.
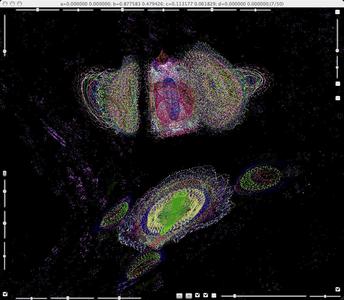b=0.877583+0.479426i, c=-0.113177+0.061829i.
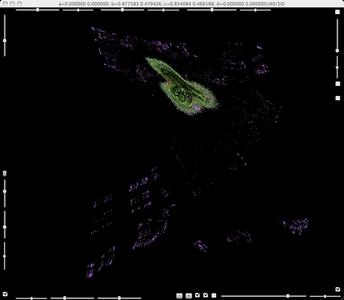b=0.877583+0.479426i, c=0.854085+0.466588i.
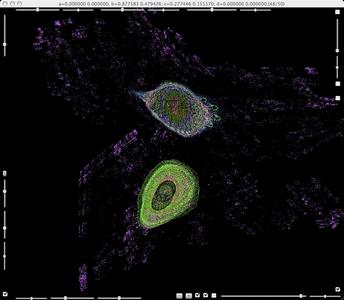b=0.877583+0.479426i, c=0.277446+0.15157i.
Family of complex Henon maps here has double identical eigenvalues of modulus one stisfying the Siegel's condition. The closure of each orbit near the elliptic fixed point are cirlces. And these circles fill a neighborhood of the fixed point.
Here we have some cases of volume preserving complex Henon maps. We say that a fixed point is parabolic-elliptic if one of the eigenvalues of the fixed point is of modulus one with irrational rotation number and another eigenvalue is a root of unity.
Family of complex Henon maps for B=-0.3 (i.e. det(H) = 0.3), with c=-1.05 to -1.45.
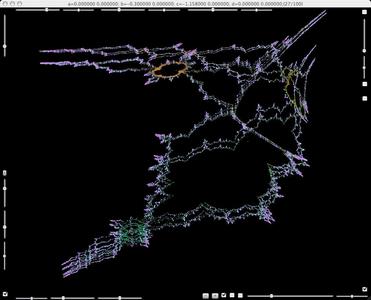Attracting periodic point of period three (Caulyflowers in orange, yellow and blue ).
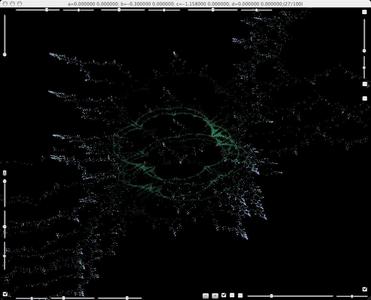Enlargement of the blue part of the above picture.
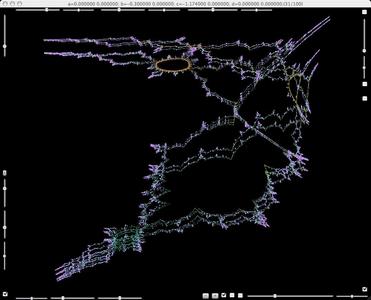Caulyflower changes its form to a round circle-like form.
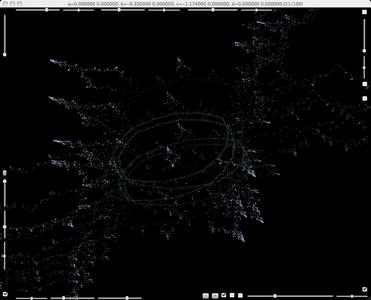Enlargement of the above. Not a Cantor set of circles, nor a solenoid.
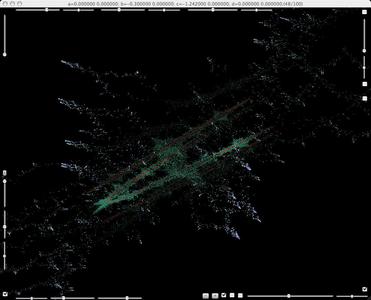After a series of bifurcations, the blue part becomes a Henon's strange attractor.
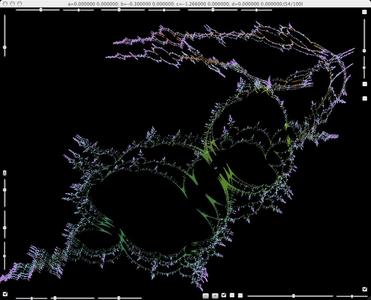The attracting fixed point becomes unstable and a period-doubling bifurcataion occurs.
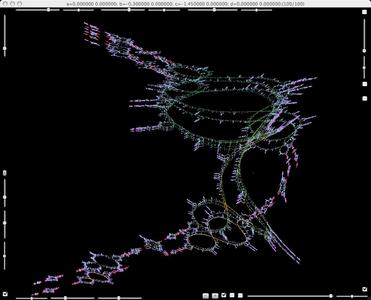The period three part is broken.
b=-1.0, c=0.6.
b=-1, c=0.4. 
b=-1, c=0. 
b=-1, c=-0.04. 
b=-1, c=-0.32. 
b=-1, c=-0.6. 
b=-1, c=-0.72. 
b=-1, c=0.4. 
b=0.3, c=-1.4. Same as above.
b=0.3, c=-1.4. 
b=0.3, c=-0.928. 
b=0.3, c=-0.992. 
Same as above.
Same as above.
Same as above.
b=1, c=-0.08.
Same as above.
b=1, c=-0.2.
b=1, c=-0.62.
Same as above.
b=0.3, c= 0.16154+0.006616i.
b=0.3, c=0.43164+0.24566i.
b=0.3, c=0.446149+0.387278i.
b=-0.3, c=0.448666+0.044873i.
b=-0.3, c=0.179546+0.421755i.
b=0.9, c= 0.376914+0.014392i.
b=0.9, c=0.430649+0.018009i.
b=0.9, c=0.886832+0.106346i.
b=0.99, c=0.229583+0.000592i.
b=0.877583+0.479426, c=-0.053716-0.029345i. Siegel-Reinhardt domans are observed. Violet points are periodic points.