Shigehiro Ushiki = Henon Julia Page
Movies of Julia sets of complex Henon maps in C2
Movies are stereo graphic. Look at the right picture with your left eye and the left picture with your right eye.
Fractal objects, "Henon Julia set" lives in complex two dimensional space, that is, in real four dimensional space.
You are looking at the projection of the object to a real three dimensional space.
The object is either rotating in the four dimensional space or changing their form according to the variation of the parameter.
Rotation in the four-dimensional space is quite different from the rotation in the three dimensional space.
The Henon mapping considered in this page is given by the following formula.
X = x^2 + c + b y
Y = x
Movies of Julia sets of complex Henon maps near saddle node bifurcation parameter.
Here we have some movies of Julia sets of complex Henon maps for b = -0.5.
The fixed point of the Henon map has a saddle node bifurcation for parameters satisfying the equation c=0.25 * (b-1)^2.
For such parameters, the fixed point has 1 as an eigenvalue.
So, for b= -0.5, the saddle node bifurcation ( parabolic bifurcation ) occurs for parameter c = 0.5625.
In our movies, when parameter c is below 0.5625, the system has an attractive fixed point. And when c is above this value, the fixed point becomes unstable and the Julia set becomes complicated.
Julia sets for volume preserving complex Henon maps
Here we have some movies of Julia sets of complex Henon maps which preserves the volume.
In the henon map with our parameters, -b is the determinant of the map.
More precisely, the algebraic determinant of the Jacobian matrix is equal to -b. And the determinant of the map regarded as a mapping of the real four dimensional euclidean space R^4, the determinant is equal to abs(b)^2.
 For c=-1.4, b=0.3, the famous Henon's Strange Attractor parameter. For this value of parameters, the Henon maps is believed to have a strange attractor in the real plane. In the complex domain, the invariant set is fractal and not an attractor in the dynamical sense. But its Julia set is a disconnected, quite complicated, fractal set. [movie4-1]1.6MB
For c=-1.4, b=0.3, the famous Henon's Strange Attractor parameter. For this value of parameters, the Henon maps is believed to have a strange attractor in the real plane. In the complex domain, the invariant set is fractal and not an attractor in the dynamical sense. But its Julia set is a disconnected, quite complicated, fractal set. [movie4-1]1.6MB
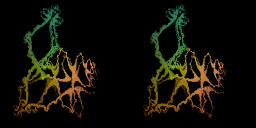 For c=-0.7, b=0.3. The Julia set is not a solenoid. The Henon map has an attractor of period two in this case.[movie4-2]1.4MB.
For c=-0.7, b=0.3. The Julia set is not a solenoid. The Henon map has an attractor of period two in this case.[movie4-2]1.4MB.
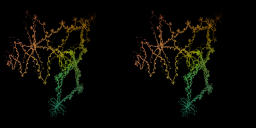 For c=-0.8, b=0.3. There is an attractor of period two. Tangential bifurcation is goung to occur. See the tangential bifurcation in the movie below. [movie4-3]2.4MB.
For c=-0.8, b=0.3. There is an attractor of period two. Tangential bifurcation is goung to occur. See the tangential bifurcation in the movie below. [movie4-3]2.4MB.
 For c=-0.9, b=0.3. The dynamical system has still an attractor of period two. Tangential bifurcation has occured. Compare the connection structure has changed by the heteroclinic tangential bifurcation. [movie4-4]2.5MB.
For c=-0.9, b=0.3. The dynamical system has still an attractor of period two. Tangential bifurcation has occured. Compare the connection structure has changed by the heteroclinic tangential bifurcation. [movie4-4]2.5MB.
 Parameter b=0.3 is fixed and parameter c is varied from -0.8 to -1.2. Observe the heteroclinic bifurcation occurs.[movie4-5]1.8MB.
Parameter b=0.3 is fixed and parameter c is varied from -0.8 to -1.2. Observe the heteroclinic bifurcation occurs.[movie4-5]1.8MB.
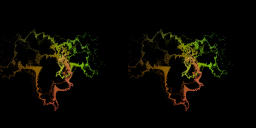 For parameter c=0.56. Below the critical value. The Julia set seems to be a solenoid. [Movie5-1]1.4MB
For parameter c=0.56. Below the critical value. The Julia set seems to be a solenoid. [Movie5-1]1.4MB For parameter c = 0.57. Above the critical value. [Movie5-2]1.4MB
For parameter c = 0.57. Above the critical value. [Movie5-2]1.4MB The value c is varied from 0.56 to 0.6.[Movie5-3]962KB
The value c is varied from 0.56 to 0.6.[Movie5-3]962KB For parameters c = 0.6, b = -1.0.
For parameters c = 0.6, b = -1.0. For parameters c = 1.0, b = -1.0.
For parameters c = 1.0, b = -1.0. For parameter b = -1.0, with c varied from 1.0 to -1.0.
For parameter b = -1.0, with c varied from 1.0 to -1.0.