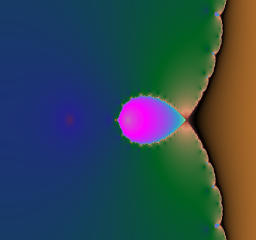

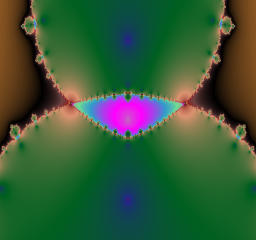

Blaschke's product map is given by the following rational function of degree three.
f(z) = z^2(z+a)/(1+bz)
Where b is the complex conjugate of parameter a.
In the movies of this page, parameter a is varied and the dynamic plane is colored according to the behavior of the points in the z plane.
Attractive basins of periodic attractors are color coded by the number of iterations befor the initial point falls in a small neighborhood of the attractor.
The points in the Herman ring or its inverse images are colored according to the distance of the orbit from the unit circle.
The module of a is 4.5 and fixed, while the argument of a is varied from 0 to pi.




The module of a is 4.1 and fixed, while the argument of a is varied from 0 to pi.


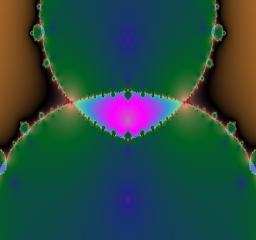

The module of a is 4.0 and fixed, while the argument of a is varied from 0 to pi.


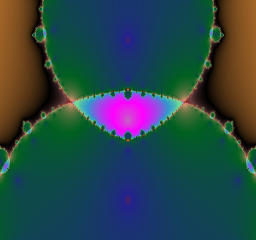

The module of a is 3.5 and fixed, while the argument of a is varied from 0 to pi.


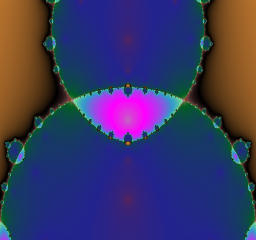

The module of a is 3.3 and fixed, while the argument of a is varied from 0 to pi.


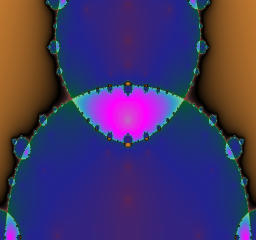

The module of a is 3.2 and fixed, while the argument of a is varied from 0 to pi.


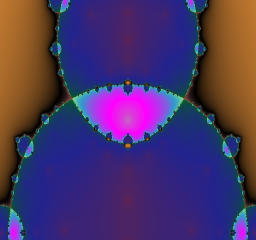
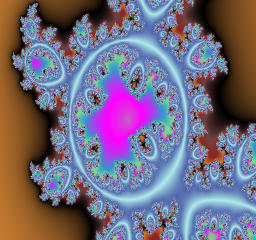
The module of a is 3.1 and fixed, while the argument of a is varied from 0 to pi.


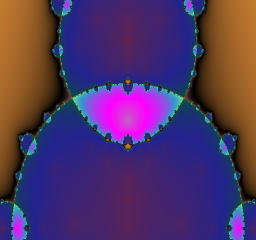

The module of a is 3.0 and fixed, while the argument of a is varied from 0 to pi.


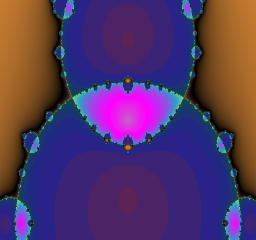

The module of a is 2.9 and fixed, while the argument of a is varied from 0 to pi.

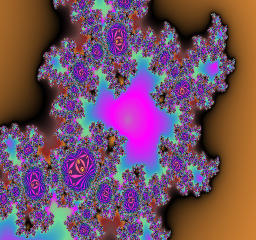


The module of a is 2.5 and fixed, while the argument of a is varied from 0 to pi.
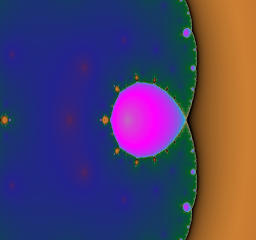



The module of a is 2.1 and fixed, while the argument of a is varied from 0 to pi.




The module of a is 2.0 and fixed, while the argument of a is varied from 0 to pi.




The module of a is 1.9 and fixed, while the argument of a is varied from 0 to pi.




The module of a is 1.7 and fixed, while the argument of a is varied from 0 to pi.



