Automorphic Representations, Automorphic Form, L-functions, and Related Topics
January 21(Mon.) – 25(Fri.), 2008
RIMS room 420, Kyoto University, Kyoto, Japan.
Abstract
I thank Kazuko Konno for making this page.
Title: Vector valued Siegel modular forms with small levels
Abstract:
On vector valued Siegel modular forms of degree 2 with respect to the symmetric tensor of degree 2, T.Satoh and T.Ibukiyama determined the structure with respect to the full modular group.
There are ten generators with some relations.
These generators are constructed from C-valued Siegel modular forms by using Rankin-Cohen-Ibukiyama differential operators.
In this talk, I will talk about the structures of vector valued Siegel modular forms with small levels.
Their structures are similar to the structure with respect to the full modular group.
Namely, there are ten generators which are constructed from C-valued Siegel modular forms by using Rankin-Cohen-Ibukiyama operators.
To prove this result, we investigate the diagonal restriction of Siegel modular forms by using another kind of differential operators.
Title: Special cohomology classes arising from the Weil representation
Abstract:
Using the dual pair Sp(n) x O(p,q), we construct certain, special,
cohomology classes for O(p,q) with values in the Weil representation.
These classes are generalizations of previous work of Kudla and Millson.
We discuss its geometric properties as Poincare dual forms for certain,
special, cycles with coefficients in a finite dimensional representation
of the orthogonal group. Moreover, globally, theta series associated to
these classes give rise to vector-valued holomorphic Siegel modular forms.
Furthermore, we also determine the behavior of the classes at the boundary
of the Borel-Serre compactification of arithmetic quotients of the
associated symmetric space for O(p,q). As a consequence we obtain certain
non-vanishing results for these cycles.
This is joint work with J. Millson.
Title: A solution of one automorphic problem of K. Saito
Abstract:
A 1-dimensional t-extension of the classical symmetric domain
of type IV was introduced in the theory of singularities by K. Saito
and E. Looijenga in 1983. In 1991 K. Saito formulated a problem
about construction of automorphic forms on this non-classical domain.
This is a question about existence of automorphic forms F(Z;t)
on the orthogonal group O(2,n) depending on additional parameter $t$.
In 1997 H. Aoki constructed the first example of such forms
using my lifting procedure for the Jacobi modular forms in n variables.
It means that there exist a t-parameter extension of the lifted
modular forms.
In this talk I would like to present a totally different approach
to the Saito problem.
THEOREM. For any modular form F(Z) of non-singular weight with respect
to the orthogonal group O(2,n) there exists its t-extension F(Z;t),
i.e, there exist a modular form F(Z;t) on the extended domain
such that F(Z;0)=F(Z).
Title: The Kodaira dimension of subvarieties of Siegel modular varieties
Abstract:
We consider codimension 1 subvarieties of Siegel modular
varieties. In principally polarized case, Freitag,
Tsuyumine and Weissauer found subvarieties of general type.
We present some subvarieties of general type in
non-principally polarized case.
Title: Hilbert-Jacobi forms of a certain index of Q(√5) (joint work with N.-P.Skoruppa)
Abstract:
Hilbert-Jacobi forms can be constructed by pair of Hilbert modular forms.
The key of this construction is Wronski type Matrix of theta series.
In the case K=Q(√5), by using this construction and
by using the structure of space of Hilbert modular fomrs,
we determined the structure of space of Hilbert-Jacobi forms of index
ε / √5 as module of Hilbert modular forms,
where O_K is principal order of Q(√5), and ε = (1+√5)/2.
Title: Principal series Whittaker functions on
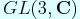
Abstract:
In this talk, we will give explicit formulas for
Whittaker functions for principal series representations of
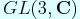 .
This is joint work with Takayuki Oda.
.
This is joint work with Takayuki Oda.
Title: Elliptic Dedekind-Rademacher Sums and Transformation Formulae of Certain Infinite Series
Abstract:
We give a transformation formula for certain infinite series in which some elliptic Dedekind-Rademacher sums arise. In the course of its proof, we also obtain a transformation formula for elliptic Dedekind-Rademacher sums. When a complex parameter  tends to
tends to 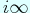 , these represent some classical results which include the reciprocity formula for Apostol-Dedekind sums.
, these represent some classical results which include the reciprocity formula for Apostol-Dedekind sums.
Title: Central L-values and periods for GL(2)
Abstract:
We will give a brief survey the problem of expressing central values of (twisted) GL(2) L-functions in terms of period integrals over compact tori (coming from the Jacquet-Langlands correspondence). Waldspurger first obtained a general formula relating these quantities, but there was also an interest in more refined formulas, such as those obtained by Gross, Zhang and others in special cases. These approaches rely on the theta correspondence, however there is also a trace formula approach to this problem initiated by Jacquet. We will end by discussing recent joint work with David Whitehouse, which follows Jacquet's approach and results in explicit formulas (a la Gross and Zhang) of the above type.
Title: 
-modular local theta correspondence
Abstract:
In this talk we will discuss about the possibility of having a local theta correspondence for 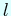 -modular representations. For the dual pair of type (Gl(n), Gl(m)) we will show a new proof, valid if
-modular representations. For the dual pair of type (Gl(n), Gl(m)) we will show a new proof, valid if 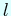 is a prime number said banal. This proof allows us to describe the correspondence in terms of Langlands parameters.
is a prime number said banal. This proof allows us to describe the correspondence in terms of Langlands parameters.
Title: Some
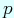
-adic properties of Siegel-Eisenstein series
Abstract:
In our previous study, we attempted to generalize the notion of Serre's 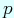 -adic Eisenstein series and obtained several interesting formulas. For example, in the Siegel modular case, a correspondence between
-adic Eisenstein series and obtained several interesting formulas. For example, in the Siegel modular case, a correspondence between 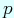 -adic Siegel-Eisenstein series and theta series was reported.
More precisely, certain
-adic Siegel-Eisenstein series and theta series was reported.
More precisely, certain 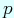 -adic Siegel-Eisenstein series were shown to coincide with the genus theta series of level
-adic Siegel-Eisenstein series were shown to coincide with the genus theta series of level 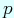 .
This indicates a remarkable relationship between
.
This indicates a remarkable relationship between 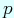 -adic Siegel modular forms and Siegel modular forms on the congruence subgroup
-adic Siegel modular forms and Siegel modular forms on the congruence subgroup
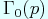 of the so-called Nebentypus.
In this talk, we show that a similar phenomenon occurs for Haupttypus.
of the so-called Nebentypus.
In this talk, we show that a similar phenomenon occurs for Haupttypus.
Title: Fourier expansion of Arakawa lifting
Abstract:
There is a theta lift to an automorphic form on 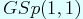 from a pair of
an elliptic cusp form
from a pair of
an elliptic cusp form 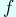 and an automorphic form
and an automorphic form 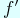 on a definite
quaternion algebra over
on a definite
quaternion algebra over
 (which we call Arakawa lifting).
The aim of this talk is to present an explicit formula for Fourier coefficients
of the theta lift in terms of toral integrals of
(which we call Arakawa lifting).
The aim of this talk is to present an explicit formula for Fourier coefficients
of the theta lift in terms of toral integrals of 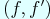 .
As an application we show the existence of non-vanishing lifts.
.
As an application we show the existence of non-vanishing lifts.
Title: Base change type spinor L-function of
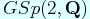
Abstract:
In the theory of automorphic representaion of 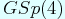 , it is known that the CAP representations (cuspidal) have the same L-functions of non-cuspidal one.
Besides, we happened to find a cuspidal representation whose spinor L-function is equal to that of non-cuspidal one.
We will determine when such a phenomenon occurs by generalizing the `Zharkovskaya relation'.
If we have time, for imaginary quadratic field
, it is known that the CAP representations (cuspidal) have the same L-functions of non-cuspidal one.
Besides, we happened to find a cuspidal representation whose spinor L-function is equal to that of non-cuspidal one.
We will determine when such a phenomenon occurs by generalizing the `Zharkovskaya relation'.
If we have time, for imaginary quadratic field 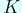 , we would like to talk about when
, we would like to talk about when 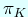 on
on 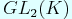 is distinguished, related to the former topic.
is distinguished, related to the former topic.
Title:Spectral square means of period integrals for wave forms on real
hyperbolic spaces
Abstract:
By using the automorphic Green function and the automorphic heat kernel,
we obtain an asymptotic behavior of the spectral square means of wave
functions on real hyperbolic spaces.
Title: An explicit construction of Jacobi forms and its applications
Abstract:
From an elliptic cusp form, we construct a Jacobi cusp form, which
gives a section of the descent map. This construction yields cusp forms in a
Maass space on orthogonal groups. As an application, we show that the
subspace of Siegel cusp forms generated by Ikeda lifts of elliptic cusp
forms can be characterized by certain linear relations among Fourier
coefficient.
Atsuo Yamauchi (Nagoya Univ.)
Title: Some vector-valued theta series on U(2,2) and Sp(1,1)
Abstract:
In this talk, we will explicitly construct some vector-valued singular forms
on U(2,2), which are generalizations of theta series.
The pull-backs of such singular forms to Sp(1,1) are modular forms generating
quaternionic discrete series, and have very simple Fourier coefficients.
These modular forms (on Sp(1,1)) can be regarded as theta series on
the hyperbolic space of dimension 4.
(This is a joint work with Hiro-aki Narita.)